testing

Manifold Flow

September 20, 2013

Engineering fluid systems consist of components and geometry that introduce challenges when attempting to accurately model the behavior. This is especially true when dealing with multiphase flow. Consider a piping system with a header that feeds multiple, parallel segments as shown in the accompanying Figure.

manifold flow

This manifold geometry is found in many spacecraft systems including radiators. For single phase flow, determining the mass flow in each leg is straightforward with a simple conservation laws but becomes challenging for two-phase flow due to the uncertainty associated with determining the phase distribution that occurs at the splitting junctions (branches). Furthermore, instabilities can occur leading to significant changes in flow conditions.

A reason for flow maldistribution in each branch is due to the momentum of each phase as it moves along the header. The high density liquid will tend to move along the header whereas the low density gas can turn into the branches. A significant amount of research has been carried out in Earth gravity with a number of different fluids, manifold geometries, and orientations but limited work has been completed for reduced gravity conditions where a lack of buoyancy impacts the phase distribution and thus, the splitting of gas and liquid at the junctions. The ITP performed some tests and modeling outlined here and some test results and model predictions are shown in the accompanying Figure.

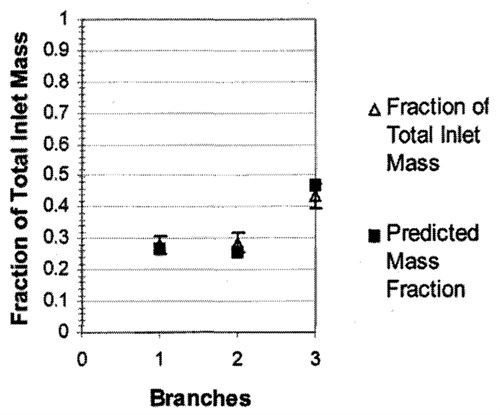
manifold test

The test consisted of a manifold with three parallel branches. The first two branches (1 and 2 in the Figure) consists of T-junctions while the last branch (branch 3) is simply an elbow. The results show that liquid preferentially moves toward the far end of the header whereas gas enters the branches at the T-junctions. A video of the testing performed on NASA’s reduced gravity aircraft can be found here. The video shows a number of interesting phenomena including changes in flow regime due to the change in gravity and changes in the mass fraction between the branch and run of the T-junction. The situation becomes more complex when one considers phase change (condensation or boiling) or other effects that upset the balance of forces. In addition, the flow velocity will differ which is further exasperated by the differences in viscosity between the phases.

Phase Separator in Operation

August 5, 2013

The vortex separator developed at Texas A&M and licensed to Advanced Cooling Technologies is a passive device with no moving parts that relies on the momentum of the incoming fluid to produce a rotational flow within the device. The flow field produces a radial acceleration that drives the separation process which can acheive high throughput compared to capillary devices. Videos of the device operating under Earth-g and during NASA reduced gravity aircraft testing show how the acceleration field can be designed to operate against gravity or to minimize the pumping power under zero gravity conditions. Another design feature is that the liquid inventory can change by controlling the gas volume within the separator which allows the device to both separate and serve as an accumulator. This feature makes the separator ideal for the DoVR radiator system since liquid and gas must be exchanged between the separator and selected radiator segments.

Using Eductor to Remove Liquid from Transport Line

August 2, 2013

A novel approach to clearing liquid from radiator lines in reduced gravity was recently demonstrated. THe approach uses a passive eductor pump and phase separator both of which have operated successfully in reduced gravity. A video of a single line being cleared using an eductor shows how effective the removal of liquid can be in an earth gravity environment. Since the dominant flow regime will be slug in zero gravity rather than slug/stratified in Earth gravity, performance should be improved. Using an appropriate arrangement of valves, eductor, and phase seperator, one could remove liquid from selected portions of the radiator which would change its heat transfer performance. A montage of the clearing process for one of the tests is shown below.